시선 예측을 위한 사용자 영상 뿐만 아니라 컴퓨터 비전의 다양한 태스크에 쓰이는 입력 영상들은 조명이나 카메라의 노출 변화에 따라 사람의 눈에 보이는 양상이 크게 변할 수 있다. 안정적이며 일관성있는 예측 성능을 얻기 위하여는 입력 영상의 밝기를 특정 범위로 제한하거나, 너무 어두운 이미지의 경우는 밝기를 조절할 필요가 있다.
어두운 조명이나 노출의 부족에 따라 광량이 부족한 이미지를 밝은 이미지로 변환하는 태스크를 light enhancement 라고 한다. 이번 포스트에서 리뷰하려는 Zero-DCE(Zero-Reference Deep Curve Estimation) 모델은 어두운 이미지를 밝게 하는 작업을 개별 이미지의 커브 예측 태스크로 생각한다. 신경망이 무겁지 않기 때문에 모바일과 같은 엣지 디바이스에서도 활용가능하도록 제안되었고, 훈련 및 추론 활용이 간단한 까닭에 케라스 예제 등을 통해 많이 소개되었다. 이 논문의 리뷰를 통해 이미지의 정보 손실을 최소화하면서 밝기를 조절하는 방법을 고찰해보려 하고, 다른 작업의 전처리로서 밝기 조절 모듈의 활용 가능성에 대하여 생각해보려고 한다.
- 논문 : Zero-Reference Deep Curve Estimation for Low-Light Image Enhancement
- 프로젝트 페이지 : Proj_Zero-DCE
- 케라스 예제 : Zero-DCE for low-light image enhancement
- 텐서플로로 구현된 깃허브 레포 : Thehunk1206/Zero-DCE
이 논문은 어두운 이미지의 광량 증가(light enhancement)를 해당 이미지에 특징적인 커브 예측 작업으로 표현하는 Zero-Reference Deep Curve Estimation(Zero-DCE)를 설명한다. 이 방식은 가벼운 심층 신경망인 DCE-Net을 학습시켜서 입력 이미지의 다이나믹 레인지를 조정하는 픽셀 마다의(pixel-wise) 고차(high-order) 커브를 예측한다. 이 때, 커브 예측은 픽셀값의 범위, 단조성, 미분가능성을 고려하여 설계되었다. Zero-DCE는 기준 영상에 대한 완화된 가정을 바탕으로 하기 때문에, 학습과정에서 짝을 이루는 데이터(paired data) 또는 각각 대응되지는 않는 집합 데이터(unpaired data)를 필요로 하지 않는다. 대신에 암묵적으로 광량 향상의 성능을 측정하고, 신경망의 학습을 이끌어내는 일련의 비참조(non-reference) 손실함수를 통하여 학습된다. 최종적으로 직관적이며 간단한 비선형 커브 매핑을 통해 이미지의 광량 증가가 수행된다.
참고) 다이나믹 레인지(Dynamic range)
표현할 수 있는 가장 어두운 정도와 가장 밝은 정도의 차이로서 명암비를 의미한다. 넓은 다이나믹 레인지를 가지게 되면, 밝은 부분과 어두운 부분을 표현하는 단계가 넓기 때문에 이미지의 디테일 관찰이 쉽고 더 많은 정보를 전달할 수 있다.
커브 조정(curve adjustment)
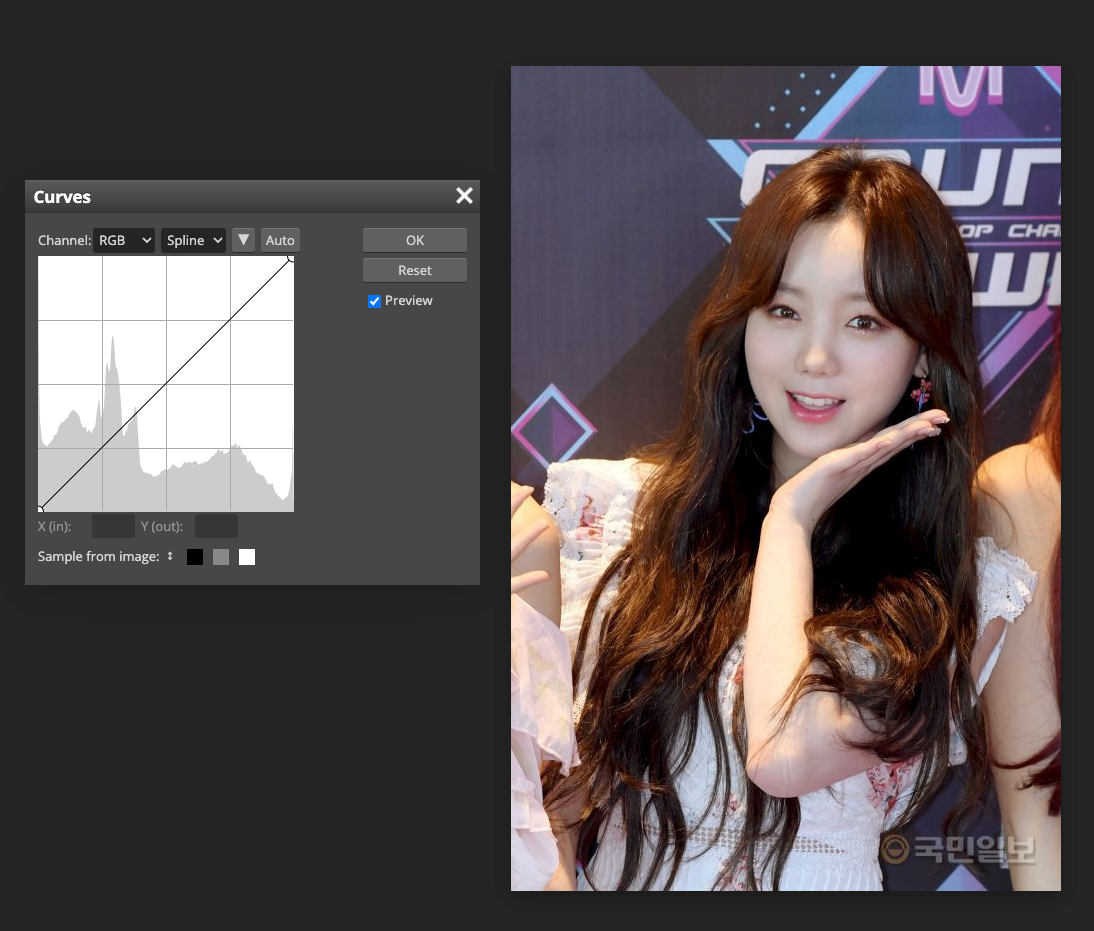
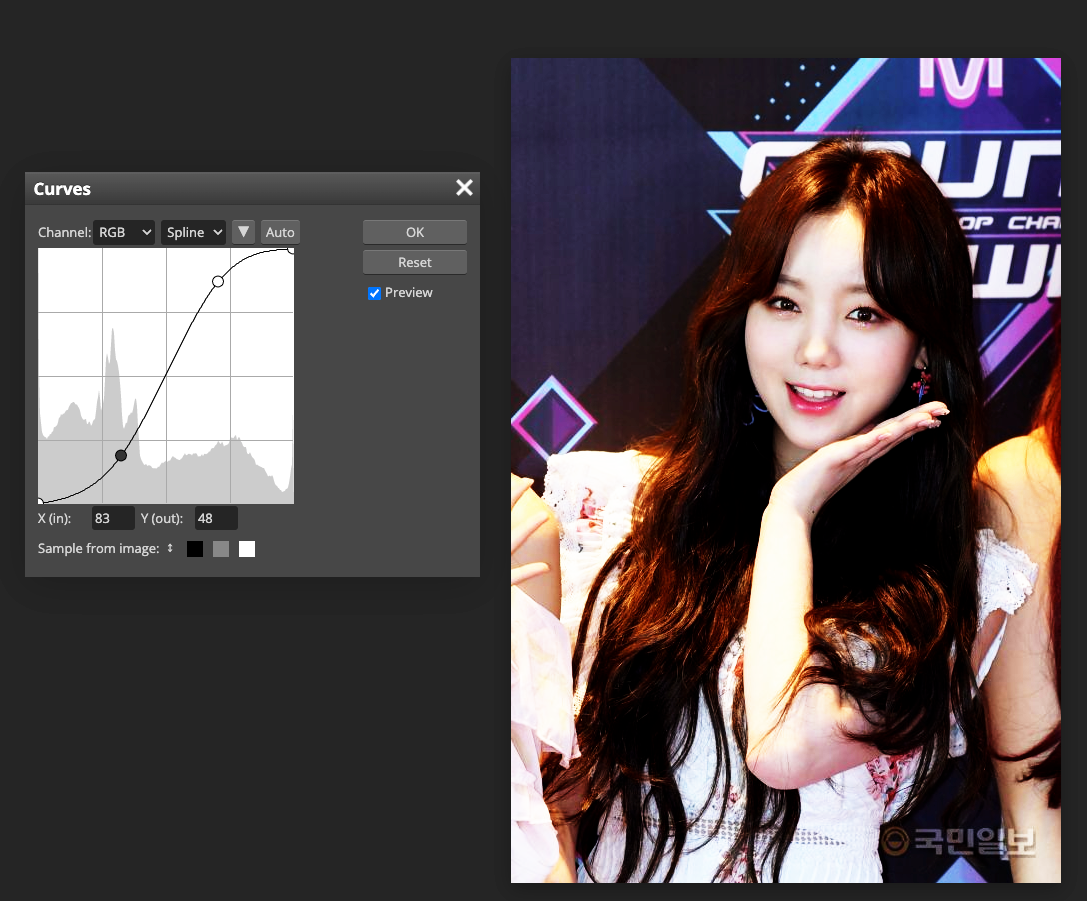
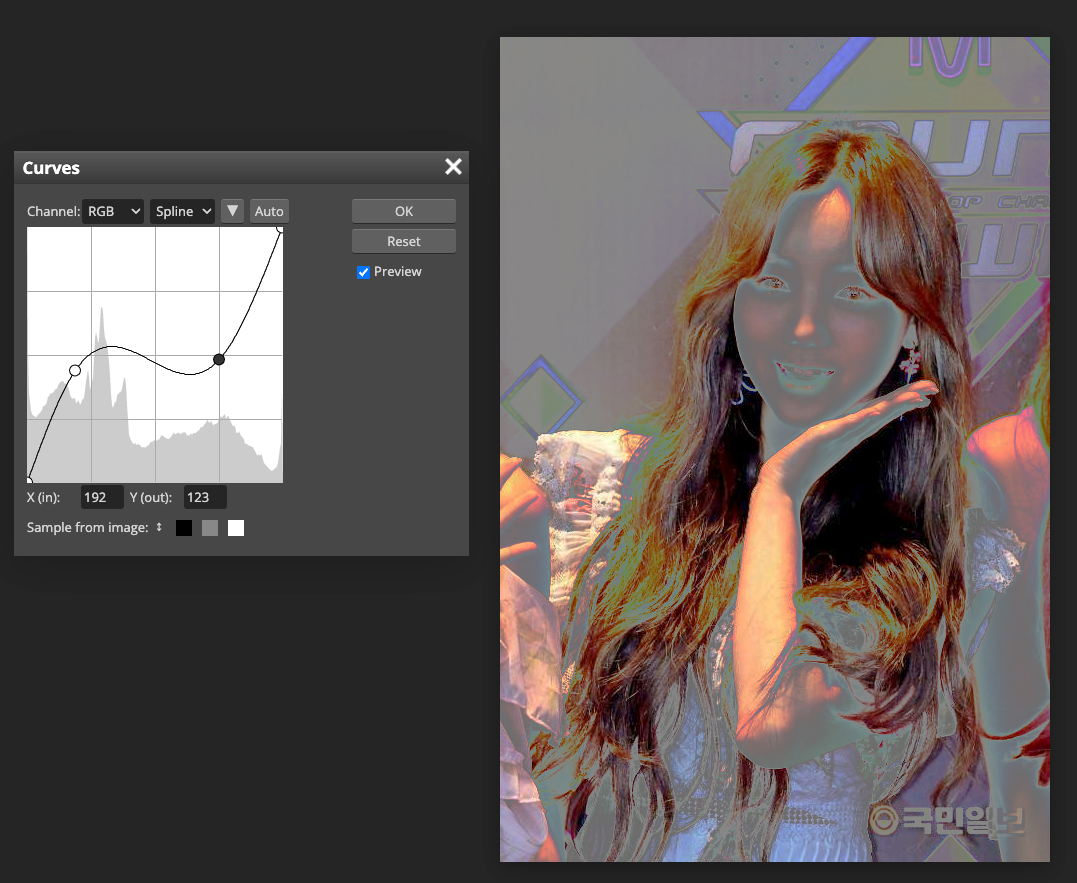
- 포토샵과 같은 이미지 편집 프로그램에서 이미지의 색조(tonality)는 직선 형태의 대각선으로 표현된다.
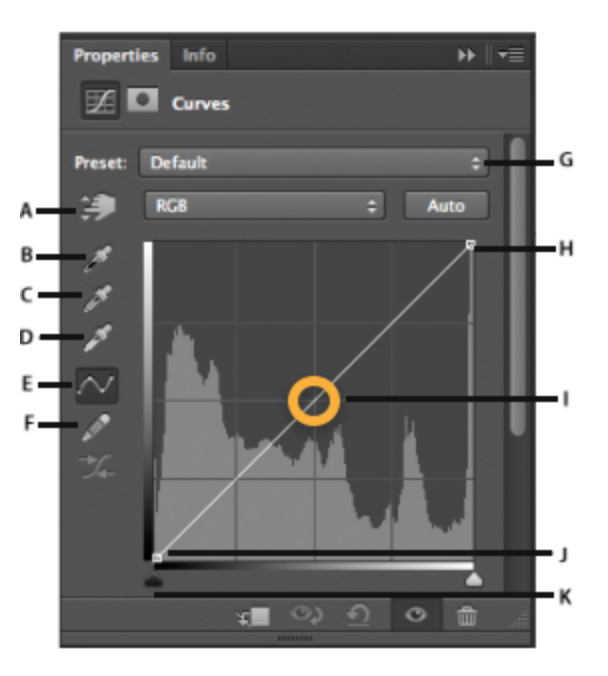
- 이미지의 색조 범위 안에 점을 추가하여서 curve adjustment가 가능하다.
- RGB이미지에서
- 오른쪽 위는 highlights 영역을 의미하고, 왼쪽 아래는 shadows를 의미한다.
- 그래프의 수평축은 원본 이미지의 입력 레벨이며, 그래프의 수직축은 출력 레벨이다.
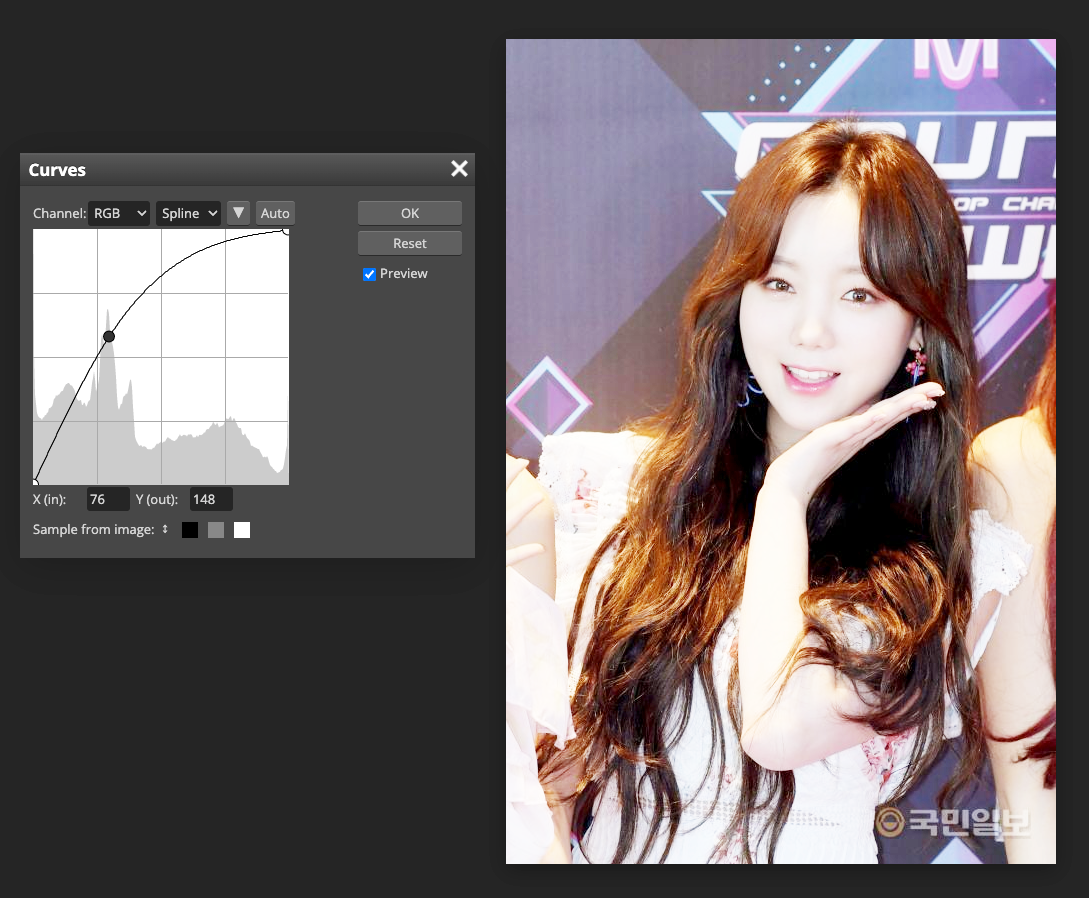
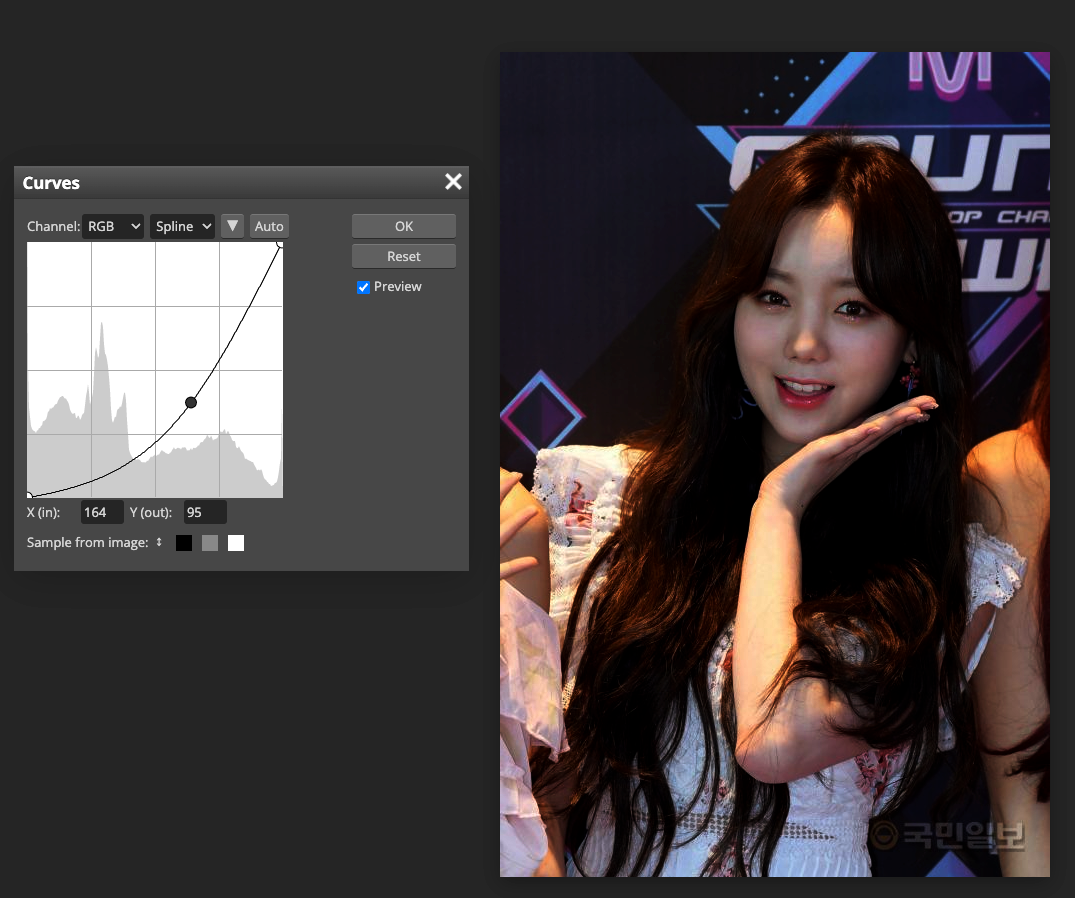
- 그래프에 점을 추가하고 움직이면, 커브의 모양이 변하면서 이미지 조정이 반영된다.
- 기울기가 큰 영역은 대비도가 높은 반면에, 편평한 영역은 대비도가 낮은 영역이다.
1. Introduction
많은 이미지들이 환경적, 기술적 한계 요인으로 인해 최적화된 조명 환경에서 획득되지는 못한다. 특히 불균형한 조명 조건이나 심한 역광 아래에서 촬영되거나 촬영 시 노출이 부족하면, 이미지가 담고 있는 정보를 충분히 전달하지 못하는 어두운 영상이 얻어지게 된다. 이 경우 객체 인식이나 얼굴 인식과 같은 작업에서는 부정확한 결과로 이어진다.
이 논문에서는 어두운 이미지의 광량 향상(low-light image enhancement)을 위한 새로운 딥러닝 기반의 방식으로 Zero-Reference Deep Curve Estimation(Zero-DCE)을 설명한다. 제안하는 방식은 어두운 이미지와 밝기가 향상된 이미지의 이미지 간 대응(image-to-image mapping)이 아닌 해당 이미지에 특징적인 커브 예측(image-specific curve estimation problem) 작업으로 문제를 재구성한다. 어두운 이미지가 입력되면 고차 커브(high-order curve)가 출력되고, 이를 이용해 입력의 다이나믹 레인지에서 픽셀 단위의 조정이 수행된다. 예측된 커브는 밝기가 향상된 이미지의 밝기 범위를 유지하면서, 인접 픽셀과의 대비도를 보존한다. 특히 커브의 미분가능한 특성 덕분에 심층 컨볼루션 신경망을 통해, 조절가능한 커브의 파라미터들을 학습할 수 있다. 이 때, 제안된 신경망이 가볍기 때문에, 예측된 고차 커브에 근사될 때까지 반복하여 적용될 수 있어서 정확한 다이나믹 레인지 조정이 가능하다.
논문에서 제안한 딥러닝 기반 방식의 독특한 장점으로 zero-reference를 꼽을 수 있다. 기존의 CNN 기반 또는 GAN 기반 방식에서 요구하는 짝을 이루는 데이터(paired data)나 각각 대응되지 않는 집합 데이터(unpaired data) 등이 학습과정에서 요구되지 않는 것이다. 이는 특별히 설계된 비참조 손실 함수들(non-reference loss functions)을 쓰기 때문인데, 광량 향상에 고려되어야 하는 여러 요인들에 관한 spatial consistency loss, exposure control loss, color constancy loss, illumination smoothness loss 가 포함된다.

이 논문의 컨트리뷰션은 다음과 같다.
- paired / unpaired data를 요구하지 않음으로써 과적합의 위험을 방지하는 광량 향상 네트워크를 제안한다. 어두운 상황 뿐만 아니라 다양한 조명 환경에도 잘 일반화된다.
- 입력 이미지에 특징적인 커브를 설계하고, 픽셀 단위의 고차 커브를 반복적으로 적용하여 밝기가 근사된다. 넓은 다이나믹 레인지 안에서 효과적인 밝기 변화가 수행된다.
- 이미지 향상에 관한 심층 모델들이 참조 이미지(reference image)가 없더라도, 해당 태스크에 특징적인 비참조 손실함수(task-specific non-reference loss functions)가 향상 품질을 간접적으로 평가함으로써 훈련에 활용될 수 있는 가능성을 보인다.
논문에서 주장하는 바에 따르면, 큰 연산 비용이 추가로 들지 않으면서 얼굴 탐색(face detection)과 같은 고수준 비전 작업의 성능을 향상시킬 수 있고, 실시간 이미지 처리가 가능하고 학습시간도 크게 소요되지 않았다. 3채널 640 x 480 이미지의 처리가 GPU에서 500FPS의 성능을 보였고, 약 30분 가량의 학습시간이 필요했다.
2. Related Work
전통적인 광량 증가 방식에는 히스토그램 평탄화(Histogram Equalization, HE) 기반 방식이 있는데, 이미지의 다이나믹 레인지를 확대하는 방법으로 어두운 이미지를 밝게 만든다. 이 때, 이미지의 히스토그램 분포는 전역(global) 수준이나 국소영역(local) 수준에서 조정될 수 있다. 또 Retinex 이론을 적용한 다양한 방법이 있는데, 통상 이미지를 반사율(reflectance) 요소와 광원(illumination)요소로 분해한다. 반사율 요소는 어떠한 광원 하에서도 일반적으로 일관적일 것으로 여겨지므로, 광량 증가 태스크는 광원 예측 문제로 표현되게 된다.
참고) Retinex 이론
인간의 시각 시스템이 장면을 인식할 때 특정 지점마다의 장면의 밝기를 인식하는 것이 아니라 주변과의 상대적 밝기를 인식한다. SSR(Single Scale Retinex)은 중앙의 픽셀값과 주변 픽셀을 포함한 컨볼루션 결과의 비율로 retinex 출력을 계산한다. 이 때, 인간의 시각 시스템이 인지하는 장면은 광원(illumination)과 물체의 반사율(reflectance)의 곱으로 인식된다는 가정이 있다.
이미지의 히스토그램을 변경하거나 부정확할 가능성이 있는 물리 모델에 기반한 전통적 방식과 달리, 제안하는 Zero-DCE 방식은 입력 이미지의 커브 매핑을 통하여 향상된 결과를 만들어낸다. 이 방식은 비사실적인 아티팩트가 생기는 일 없이 영상을 밝게 할 수 있다. 자동적으로 노출을 수정하는 이전 연구에서는 주어진 이미지의 S자 형태의 커브를 전역 최적화 알고리즘으로 예측하고, 각 분할된 영역을 커브 매핑을 통해 최적화 영역으로 바꿔줬다. 이 연구와 달리 Zero-DCE는 순수하게 입력 데이터에 의해 주도되는 방식이며, 다수의 밝기 영향 요소들이 고려되어 비참조 손실함수로 같이 표현된다. 이에 따라 더욱 일관성있는 결과와 더 넓은 다이나믹 레인지로 조정이 가능하면서, 연산 부담을 적어졌다.
사용하는 데이터를 활용하는 방식에 따라 CNN기반 방식과 GAN 기반 방식으로 분류해 볼 수도 있다. 대부분의 CNN 기반 방식은 대응되는 (어두운 이미지)-(밝은 이미지)로 구성된 paired data를 활용하는 지도 학습(supervised training)을 사용한다. 보통 짝을 이루는 데이터는 자동적인 광량 저하, 데이터 수집 시 카메라 설정 변화 등을 통해 시간을 들여 수집되거나, 이미지 리터칭을 통해 합성된다. LOL 데이터셋은 노출 시간과 ISO를 변화시킨 어두운 이미지와 정상 이미지의 쌍으로 구성되어 있고, MIT-Adobe FiveK 데이터셋은 5,000장의 원본(raw) 이미지와 전문가에 의해 리터치된 각 5장씩의 이미지로 구성되어 있다.
최근에 광원 맵(illumination map)을 예측함으로써 노출 부족된 사진을 향상시키는 신경망이 제안되었다. 이 신경망은 세 명의 전문가가 리터치한 쌍 데이터로 훈련되었다. 그런데 우리는 이러한 쌍 데이터를 통해 훈련된 신경망이 비현실적이라고 생각할 수 있다. 충분한 paired data를 수집하기 위해 높은 비용이 필요하며, 데이터 생성 과정에서 인위적이고 비현실적인 데이터가 포함되기 때문이다. 이런 점 때문에 CNN 기반 방식의 일반화 성능이 늘 만족스럽지 못했다. 다양한 광량의 실제 이미지에 적용되었을 때, 아티팩트나 잘못된 색상 변화가 생성되는 경우가 많았다.
이에 비해 비지도 GAN 기반 방식은 훈련에서 쌍 데이터를 활용하지 않는다는 장점을 가지게 된다. EnlightenGAN은 비지도 GAN기반 방식으로 각각 대응되지 않는 정상/어두운 이미지 집합데이터(unpaired low/normal data)를 사용한 선구자적인 연구다. 정교하게 설계된 판별자와 손실 함수를 통해 신경망을 학습시켰다. 비지도 GAN기반 방식은 쌍 데이터를 요구하지는 않지만, unpaired data를 신중하게 선택해야한 했다.
제안하는 Zero-DCE는 적어도 세가지 측면에서 기존 CNN기반, GAN기반 방식보다 월등한 성능을 가지고 있다. 첫째로 참조가 필요없는 zero-reference 학습 전략을 가짐으로써, paired / unpaired data의 필요성을 없앴다. 다음으로 비참조 손실함수를 정의하여 훈련되고, 출력된 영상의 품질이 암묵적으로 평가되어서, 신경망 학습에 반복해서 사용 도록 한다. 마지막으로 Zero-DCE는 가벼운 신경망 구조를 가져서 연산 비용 측면에서 효율적이다.
3. Methodolgy
Zero-DCE를 모식화하면 다음 그림과 같다.

DCE-Net(Deep Curve Estimation Network)는 주어진 입력 이미지에 대해 가장 잘 맞는 광량 향상(Light-Enhancement) 커브를 평가한다. 그 후 프레임워크는 입력이미지의 RGB 채널의 모든 픽셀에 반복적으로 커브를 적용하여서 최종 향상된 이미지를 얻는다.
3.1. Light-Enhancement Curve(LE-Curve)
이미지 편집 소프트웨어의 커브 조정(curve adjustment) 방식에서 영감을 얻어, 어두운 이미지를 자동으로 광량이 향상된 상태로 대응시키는 커브를 설계하려 했는데, 이 때 자기-적응적인 커브 파라미터들(self-adaptive curve parameters)는 오직 입력 이미지에 의해서만 결정되게 된다. 이 때, 커브가 갖춰야할 목표로 3가지 사항을 꼽을 수 있었다.
- 밝아진 이미지의 픽셀값은 정규화된 [0, 1] 범위 안에 있어야만 overflow truncation(범위를 벗어난 오버플로 발생시, 범위에 맞추기 위해 값이 버려지는 경우)에 의한 정보 손실을 방지할 수 있다.
- 커브는 단조성(monotonous)을 유지하여야만 인접한 픽셀들과의 차이, 즉 대비(contrast)를 보존할 수 있다.
- 커브의 형태는 가능한 한 단순하며, 역전파 과정을 위해 미분가능(differentiable)해야 한다.
이러한 3가지 목표의 달성을 위해, 설계된 이차 커브의 수식 표현은 아래와 같다.
$$ LE( I( \mathbf{x} ); \alpha) = I (\mathbf{x}) + \alpha I(\mathbf{x}) ( 1 - I(\mathbf{x})) $$
여기서 $\mathbf{x}$는 픽셀의 좌표를 말하고, $LE( I(\mathbf{x}) ; \alpha) $는 주어진 이미지 $I(\mathbf{x})$에 대해 광량이 향상된 이미지다. $\alpha \in [-1, 1] $는 학습가능한 매개변수로서 LE-curve의 강도를 조절하고, 노출 레벨을 조정한다. 모든 픽셀은 $[0, 1]$로 정규화되며, 모든 연산은 픽셀 마다 수행된다. LE-curve는 단독으로 illumination 채널에 적용되는 대신에, 3개의 RGB 채널에 개별적으로 적용되는데, 이러한 3채널 조정은 원래의 색상을 더 잘 보존할 수 있게 하며 채도가 과도해지는 over-saturation의 위험성을 줄여준다.
$\alpha$ 값의 변화에 따른 LE-Curve의 형태가 위의 모식도(b)에 나타나 있다. ( (더보기)에서 설명한 것처럼, 통상 가로축은 입력이미지의 픽셀 입력 레벨이고, 세로축은 여기에 대응되는 출력 레벨이다.) 추가적으로, LE-Curve는 입력 이미지의 다이나믹 레인지를 확장하거나 축소할 수 있는데, 이 덕분에 어두운 영역을 밝게 만들 수 있을 뿐만 아니라 과도하게 노출된 아티팩트를 제거할 수 있다.
만약 LE-Curve가 반복해서 적용된다면, 더욱 어두운 상황에서 얻어진 이미지에도 유연하게 적용될 수 있다.
$$ LE_n ( \mathbf{x}) = LE_{n-1} (\mathbf{x}) + \alpha_n LE_{n-1}(\mathbf{x}) ( 1-LE_{n-1}(\mathbf{x})) $$
$n$은 반복 횟수로서 커브의 곡률을 조절한다. 이 논문에서는 대부분의 어두운 이미지에서 만족스러운 결과를 내놓는 $n=8$로 설정한다. 모식도(c)는 $n=4$ 일 때, $\alpha_1, \alpha_2, \alpha_3 $은 $-1$로 정한 후, $\alpha_4$를 변화시켜가면서 측정한 결과다. 이로부터 더 큰 곡률을 갖는 고차 커브가 훨씬 강력한 광량 조정 효과가 있음을 알 수 있다.
이처럼 고차 커브를 활용하면 더 넓은 다이나믹 레인지에서 이미지 조정이 가능하다. 한편, 위의 식에서 $\alpha$가 모든 픽셀에 공통적으로 사용되는 값이므로, 전역적인 조정(global adjustment)에 해당한다. 그런데 이런 전역적인 매핑은 국소 영역에서 과소하거나 과도한 광량 향상으로 이어질 수 있다. 이런 문제를 해결하기 위해서, 논문은 $\alpha$를 픽셀마다의 파라미터(pixel-wise parameter)로 설정하여서, 이미지의 각 픽셀이 저마다의 $\alpha$를 가지고 대응되는 커브를 갖게 하였다.
$$ LE_n ( \mathbf{x}) = LE_{n-1} (\mathbf{x}) + \mathcal{A}_n LE_{n-1}(\mathbf{x}) ( 1-LE_{n-1}(\mathbf{x})) $$
$\mathcal{A}$는 입력 이미지와 같은 크기의 파라미터 맵이다. 여기에서 국소 영역의 픽셀들은 같은 강도(밝기, intensity)를 갖고 있고, 또한 같은 조정 커브를 갖는다고 가정함으로써, 밝기가 향상된 출력 이미지도 단조성을 유지하게 된다.

위 그림은 한 어두운 이미지에서 각 채널별로 예측된 커브 파라미터 맵을 보여준다. 서로 다른 채널들은 비록 유사한 조정 경향을 가지지만, 최적의 파라미터 맵의 값들은 다르다는 것을 알 수 있다. 커브 파라미터 맵은 벽의 반짝이는 지점들을 포함해 서로 다른 영역의 밝기를 정확하게 나타낸다. 이제 픽셀마다의 커브 매핑을 통해 밝기가 향상된 이미지를 바로 얻을 수 있다.
3.2. DCE-Net
DCE-Net을 통하여 입력 이미지와 최적의 커브 파라미터 맵의 대응관계가 학습된다. DCE-Net의 입력인 어두운 이미지에 대하여, 대응되는 고차 커브에 따른 픽셀 마다의 커브 파라미터 집합이 출력된다. 아키텍처는 대칭적으로 연결된(symmetrical concatenation) 7개의 컨볼루션 레이어로 구성된 CNN이다. 각 레이어는 스트라이드 1의 3x3 크기의 커널 32개를 통과시킨 후 각각 ReLU 활성화함수를 적용한다. 다운 샘플링과정이나 배치 정규화를 적용하지 않음으로써, 이웃 픽셀과의 관계가 깨지지 않도록 하였다. 최종 컨볼루션 레이어의 활성화함수는 tanh를 적용한다. 8번의 반복이 끝나면 24개의 파라미터 맵을 얻게 되는데, 각 반복에서 3채널 각각 마다 하나의 파라미터 맵이 생성되기 때문이다.
DCE-Net의 훈련가능한 매개변수 수는 79,416개로 256 x 256 크기의 3채널 이미지에 대하여 5.21 GFlops로 연산될 수 있다. 이처럼 DCE-Net은 가벼운 경량모델이므로, 모바일과 같은 연산자원이 제한된 환경에서도 사용될 수 있다.
3.3. Non-Reference Loss Functions
앞서 언급된 것처럼 DCE-Net이 참조 이미지 없이 zero-reference 학습을 하려면, 향상된 이미지의 품질을 평가하는 비참조 손실 함수(non-reference loss functions)가 정의되어야 한다. 이에 따라 다음의 4가지 손실함수가 모델 학습을 위하여 적용되었다.
1. Spatial Consistency Loss ($L_{spa}$)
입력이미지와 밝기가 향상된 이미지에서 이웃한 영역과의 차이를 보존함으로써, 밝아진 이미지의 공간적 일관성(spatial coherence)이 유지되게 한다.
$$ L_{spa} = \frac{1}{K} \sum_{i=1}^K \sum_{j \in \Omega(i)} (| (Y_i - Y_j)| - | (I_i - I_j)|)^2 $$
$K$는 국소 영역의 수이며, $\Omega(i)$는 $i$ 번째 국소영역의 (위, 아래, 오른쪽, 왼쪽)의 4곳의 인접영역을 뜻한다. $Y$와 $I$는 각각 밝아진 이미지와 원본 입력 이미지에서 평균 밝기(intensity) 값이다. 논문에서는 실험적으로 국소 영역의 크기를 4x4로 정했는데, 다른 크기로 지정되더라도 $L_{spa}$는 안정적이었다.
2. Exposure Control Loss ($L_{exp}$)
노출 레벨을 조절하여서 과소 노출되거나 과대 노출된 영역을 제한한다. 국소 영역의 평균 밝기 값과 적정 노출레벨(well-exposedness level) $E$와의 거리를 측정한다. 이 때, 기존의 연구에서처럼 RGB 색공간에서 회색이 나타내는 밝기(gray level)를 $E$로 설정하였고, 논문의 실험에서는 0.6으로 정하였다.
$$ L_{exp} = \frac{1}{M} \sum_{k=1}^M | Y_k - E | $$
$M$은 서로 겹치지 않는 16x16 크기의 국소영역의 수이며, $Y$는 밝아지 이미지에서 국소영역의 평균 밝기 값이다.
3. Color Constancy Loss ($L_{col}$)
각 센서 채널의 색상은 전 이미지 영역에서 평균을 내면 회색이 된다는 Gray-World color constancy hypothesis을 따라, 밝기가 향상된 이미지에서 생길 수 있는 색상 이탈(color deviation)을 수정할 수 있는 색상 불변성 손실(color constancy loss)을 설계한다. 이 손실은 동시에 새롭게 조정된 채널들 간의 관계를 설정해 준다.
$$ L_{col} = \sum_{\forall (p,q) \in \varepsilon} ( J^p - J^q)^2 ~, \varepsilon = \{ (R, G), (R, B), (G, B) \} $$
$J^p$는 밝기가 향상된 이미지의 p 채널의 평균 밝기 값이며, $(p, q)$는 채널 쌍을 뜻한다.
4. Illumination Smoothness Loss ($ L_{tv \mathcal{A}} $)
이웃 픽셀과의 단조성을 유지하기 위하여, 각 커브 파라미터 맵 $\mathcal{A} $에 추가한다.
$$ L_{tv \mathcal{A}} = \frac{1}{N} \sum_{n=1}^N \sum_{c \in \xi} (| \nabla_x \mathcal{A}^c_n | + |\nabla_y \mathcal{A}^c_n|)^2 , \xi = \{ R, G, B \}$$
$N$은 반복횟수이며, $\nabla_x, \nabla_y $는 각각 수평(horizontal), 수직(vertical) 그래디언트 연산이다.
위의 비참조 손실함수들이 합쳐진 최종 손실은 다음과 같다.
$$ L_{total} = L_{spa} + L_{exp} + W_{col} L_{col} + W_{tv \mathcal{A}} L_{tv \mathcal{A}} $$
4. Experiments
넓은 다이나믹 레인지에 대한 조정이 이뤄지도록, 훈련 데이터셋에는 어두운 이미지뿐만 아니라 과노출된(over-exposed) 이미지도 포함시켰다. EnlightenGAN의 학습에도 활용되었던 SICE(Single Image Contrast enhancement) 데이터셋의 Part1: 360 multi-exposure sequences를 이 목적을 위해 활용하였다. 서로 다른 노출 레벨을 가진 3,022장의 이미지 중에서 2,422장을 훈련셋에 쓰고, 나머지를 검증셋에 사용하였다. 훈련 이미지는 512x512 크기로 리사이즈 시킨다.
NVIDIA 2080Ti에서 PyTorch로 구현된 코드를 실행하였다. 이 때, 배치 크기는 8로 설정되었고, 각 레이어의 초기 가중치는 평균 0, 표준편차 0.02의 가우시안 함수로 초기화되었다. 기본 파라미터 변화없이 ADAM을 옵티마이저로 사용하고, 고정된 학습률 $1e^{-4}$로 학습되었다. 앞서 설명된 최종 손실에서 손실에 대한 가중치 $W_{col}$과 $W_{tv \mathcal{A}} $는 각각 0.5, 20으로 설정하였다.
4.1. Ablation Study
비참조 손실 함수들의 구성을 바꾸면서 실험하여서, 각각의 손실함수가 훈련에 미치는 영향을 살펴본다.

우선, spatial consistency loss $L_{spa}$가 없이 훈련되면, 상대적으로 결과이미지의 대비도가 낮아진다. 구름 영역에서 나타나는 것처럼, 이웃 영역과의 차이가 보존되게 하려면 $L_{spa}$가 중요한 역할을 한다. 두번째로 exposure control loss $L_{exp}$가 없으면, 어두운 영역의 밝기가 개선되지 않는다. color constancy loss $L_{col}$가 없으면, 예상하지 못한 색상 변화가 일어날 수 있다. 이 변화는 커브 매핑이 일어날 때, 3채널 간의 관계성을 무시할 수 있다. 마지막으로 illumination smoothness loss $L_{tv \mathcal{A}}$가 제거되면, 이웃 영역과의 상관관계가 깨져서 확연한 아티팩트가 나타나게 된다.
두번째로 DCE-Net의 깊이(depth: 컨볼루션 레이어의 수)와 너비(width: 한 레이어에서 사용되는 필터의 수) 그리고 반복횟수와 같은 DCE-Net의 파라미터들의 효과를 평가한다.

(b)의 그림으로부터 3개의 컨볼루션 레이어만을 사용하더라도, 이미 어느정도 광량이 향상된 결과를 보임을 알 수 있다. 그럼 (e)와 (f)가 가장 시각적으로 자연스러운 노출과 적절한 대비를 갖는 결과를 보여서, 반복 적용의 효과를 알 수 있다. 이에 비해 (d)처럼 반복적용횟수가 1회가 되면, 광량향상의 성능이 저하됨을 알 수 있다. 이는 단일한 커브 적용은 제한된 조정 효과를 가진다는 의미다. 결국 (반복에 따라 적용 결과가 달라지는) 고차 커브 예측이 필요하며, 논문에서는 성능상의 효율성과 원본 이미지의 정보를 그대로 보존하는 복원 성능이 잘 조화되는 $\text{Zero-DCE}_{7-32-8}$을 최종 모델의 파라미터로 선택하였다.
마지막으로 Zero-DCE를 서로 다른 데이터셋에서 훈련시킴으로써, 훈련데이터 선택의 효과를 살펴본다. 각 데이터셋과 그로부터 훈련된 모델은 다음과 같다.
- $\text{Zero-DCE}_{Low}$ : 훈련데이터로 분류된 2422장 중에서 900장의 어두운 이미지만 사용
- $\text{Zero-DCE}_{LargeL}$ : DARK FACE 데이터셋에서 9000장의 레이블되지 않은 이미지를 사용
- $\text{Zero-DCE}_{LargeLH}$ : SICE 데이터셋의 Part1과 Part2에서 data augmentation으로 확장된 4800장의 여러 노출 상태의 이미지를 사용

과대노출된(over-exposed) 훈련데이터가 포함되지 않은 데이터로 학습될 경우, 어두운 이미지에서도 밝았던 영역은 (c)와 (d)의 얼굴 영역처럼 과하게 밝하지게 된다. 이는 어두운 이미지의 수가 많아지는 것만으로는 해결되지 않았다. 따라서 노출 상태가 다양한 multi-exposure 훈련 데이터가 DCE-Net의 학습에 사용될 필요가 있음을 알 수 있었다. 이 때, multi-exposure 데이터의 양이 늘어나면 (e)의 경우처럼 어두운 영역이 더욱 잘 밝기 향상이 될 수 있음도 관찰되었다.
4.2. Benchmark Evaluations
논문에서는 Zero-DCE를 전통적인 밝기 향상 방법, CNN기반 방식, GAN기반 방식과 비교하였다. 이 때 사용된 이미지셋은 NPE(Naturalness Preserved Enhancement) 데이터셋 84장, LIME(Low-light IMage Enhancement via illumination Map Estimation) 데이터셋 10장, MEF(Multi-Exposure image Fusion) 데이터셋 17장, DICM 데이터셋 64장, VV 데이터셋 24장 등이다.
참고) Low-light Image Enhancement Benchmarks
'A.I. > 이론' 카테고리의 다른 글
| LLM)논문꼼꼼히읽기 - A Survey of Large Language Models (1) | 2024.07.05 |
|---|---|
| 논문 번역 및 요약) LLM을 활용한 문학 번역 - (Perhaps) Beyond Human Translation (0) | 2024.05.27 |
| 논문 리뷰)시선 예측 연구의 고전 - Eye Tracking for Everyone (1) | 2022.08.20 |
| 시선 예측을 위하여 딥러닝 기술은 어떻게 활용 되는가? (0) | 2022.04.24 |
| 논문요약)Improved Regularization of Convolutional Neural Networks with Cutout (0) | 2020.07.21 |


댓글